【書評】『問題解決大全』(読書猿)
お薦めの本の紹介です。
読書猿さんの『問題解決大全――ビジネスや人生のハードルを乗り越える37のツール』です。
読書猿(どくしょざる)さんは、正体不明・博覧強記の読書家です。
人気ブログ、読書猿Classic: between / beyond readersの執筆者でもあります。
問題解決は、「方法を生み出す方法」である
読書猿さんは、問題解決の技術は、人間が限界である存在であることを自覚しながら、今の能力を超えた問題から逃げず、立ち向かおうとするところに生まれる
と述べています。
つまり、問題解決の技術は〈方法を生み出す方法〉
だといえます。
問題解決をできるだけやさしく、また広く定義すれば、自分で定めた目標に向かってうまく行動すること、言い換えれば「〜したい」と思うことを実現すること、だと言える。
目標を抱くこと、その実現のために自分の行動を計画し実行することはまた、人間の能力であると同時に人間が人間たるための条件でもある。
我々が互いを一人前の人間として扱うのは、互いに責任を問える存在として考えられるとき、すなわち責任主体と見なせるときに限られる。
そして人が責任主体となるのは、その人が自由に自身の意図を抱くことができ、その意図を実現するために行動することができる場合である。
この意図の実現を目指す行動を我々は問題解決と呼ぶ。
(中略)
しかし我々は、問題に関するすべてを把握できるわけでもコントロールできるわけでもない。人間は全知でも全能でもない。失敗の原因には、我々には知り得なかったもの、予見できたとしてもどうすることもできなかったものも、含まれうる。
つまり問題解決者は、問題解決の結果について責任を負うならば、自身の知や力を超えた事柄についても、その帰結を引き受けなくてはならないことになる。
予見もコントロールもできなかった事柄とその帰結についてすら、自らの責任として引き受けることは過大な要求ではある。しかし、人はそうすることで、将来における同種の行動についてのコントロールの可能性を増大させ、自身の自由の範囲を拡張することができる。
全知でも全能でもない人が自由でありうるのは、この限りにおいてである。
そして問題解決が自身を拡張する再帰性を備える意義は、ここに存する。『問題解決大全』 第1部 より 読書猿:著 フォレスト出版:刊
本書は、困難や窮状を「問題」として捉え直し、その対処法や目標へ到達するための手段・方法を実行することで、未来を変える方法と知恵
を体系化してまとめた一冊です。
その中からいくつかピックアップしてご紹介します。
[ad#kiji-naka-1]
不安で仕方なくなったときの対処法
深刻な問題や、差し迫った課題に直面し、不安で仕方なくなったとき。
私たちは、その状況から逃げたり、目を背けたりしがちです。
それを回避するための問題解決法が、「100年ルール」です。
■問題を前にしたとき、災難に見舞われたとき、不安で仕方なくなったときに、以下のように自問自答する。
「これは100年後にも重大なことか?」
「これは100年後にも誰かに記憶されていることか?」
100年が長すぎる場合は、30年や5年など、より短い時間を用いてもよい。
この変種で、極めて短い時間を設定するものもある。こちらも予期不安から問題を過大視している場合に効果がある。
「これは5分後も重大な問題か?」
5分後という短い確定した時間内では、不安をもたらす何事も現実には生じないことが確認できる。テストに対する不安を解消したい
テスト不安は多くの人が経験する一般的なものだが、こじれると試験のための準備も手につかず、そのせいでさらに不安が高まる、という悪循環に陥ってしまう。最悪の場合、不安から逃れるため、試験を受けることを放棄するようになる。
なんとか試験期間を耐えしのげは、当然、一時的には不安は消えるだろう。しかし、次の試験まで何の対策もせずに過ごすと、数ヶ月後、また同じ悪循環に陥ることになる。
テスト不安の背景にはテストに失敗することへの恐れ、成功せねばという信念と、ここから生まれる緊張、他者に評価されることへの心配などが存在する。
不安のために準備が手につかないという状況を打破するため、ここでは「100年ルール」では長すぎるので、5年ルールを使ってみよう。
Q「次のテストは5年後にも重大なことか?」
A「5年の間にはもっと重要な入学試験が過ぎている。次回の小テストはそれに比べれば影響があるにしてもずっと小さい」さらに5分ルールもやっておこう。
Q「次のテストは5分後には重大な問題か?」
A「5分後にはテストはまだ始まっておらず、今と状況は変わっていない。テストまで、あと48時間以上ある。・・・・・恐れているのはテストの結果が悪いことで・・・・・だから、少なくともテストまでは、いやテストの結果が返ってくるまでは、実際のところ何か悪いことが起こるわけではない」『問題解決大全』 第1部 より 読書猿:著 フォレスト出版:刊
とても心配なことがあると、そのことに意識がフォーカスし、視野が狭くなりがちです。
そんなときにこそ、「100年ルール」です。
より高い視点で眺めることで、問題を客観的に捉える効果があります。
いろいろな場面で、応用できそうですね。
「未知なるもの」を推定する方法
データが不足しているが、何らかの判断を下したい。
曖昧なイメージや直観を、とにかく数値に変換したい。
そんなときに役立つのが、「フェルミ推定」です。
フェルミ推定は、物理学者エンリコ・フェルミ(1901–1954)が開発したもので、桁数の推定を目標とした方法です。
シカゴにあるピアノの台数を探る
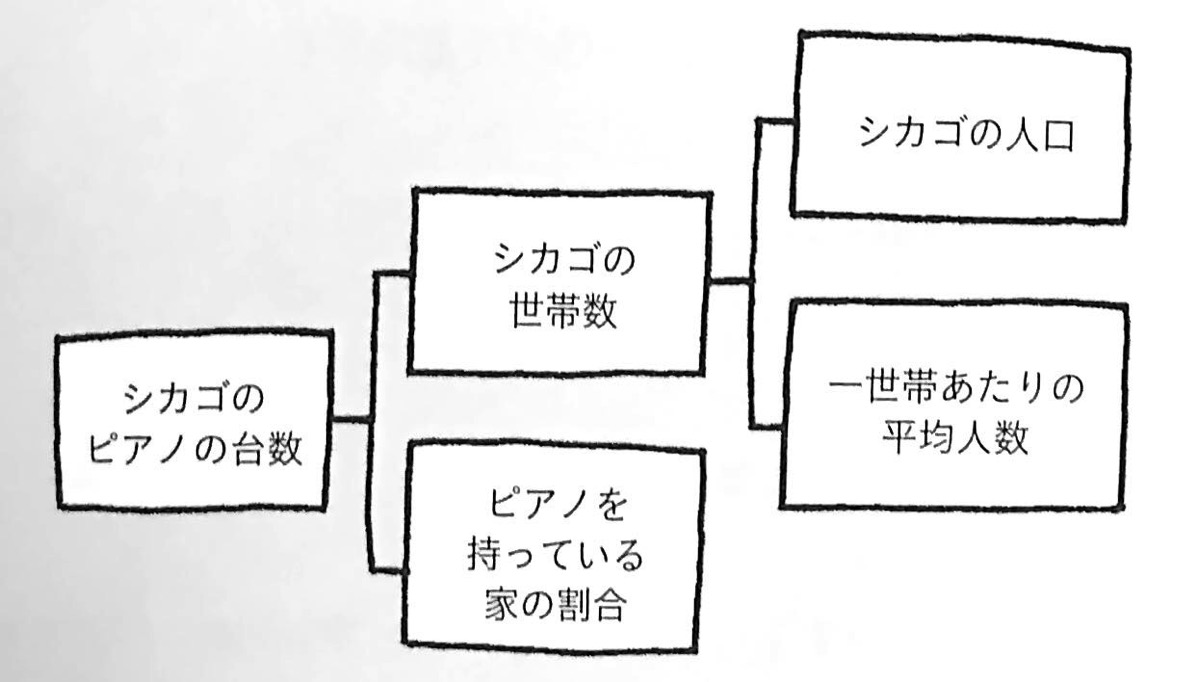
まずはフェルミ問題の例として必ず取り上げられる問題を簡略化して「シカゴにあるピアノの台数」をフェルミ推定してみよう。①桁数の推定を目標にする。
②問題を分割し、次のようなツリーをつくる
③ロジック・ツリーの枝の先端から数値を推定する。
①知っている/利用できる数値を使う。
あなたがシカゴの人口を知っているなら、またピアノを持っている家の割合を知っているなら話は早い。しかしここでは不幸にも、どの数値も知らないとしよう。②知らない数値が必要な場合は上限と下限から考えて、その幾何平均(相乗平均)を取る。
今の「シカゴの人口」だと、確かに何人かはわからないが、しかしシカゴはどこかの寒村ではなく、結構な大都市であることは、おぼろげながら知っているだろう。
こうした場合、この「おぼろげながら知っていること」を間違ってはいない程度の数値に落とし込む方法がある。
まず下限を考える。シカゴの人口が、何十万人(=105)というのは、どうにも少なすぎる。というのも、何十万人では、いくらでもある普通の地方都市レベルだからだ。
次に上限を考える。桁違いな数字を考えて、何千万人(=107)ではどうか? いやこれは多すぎる。これだと世界にいくつかしかない屈指の都市レベルになってしまう。
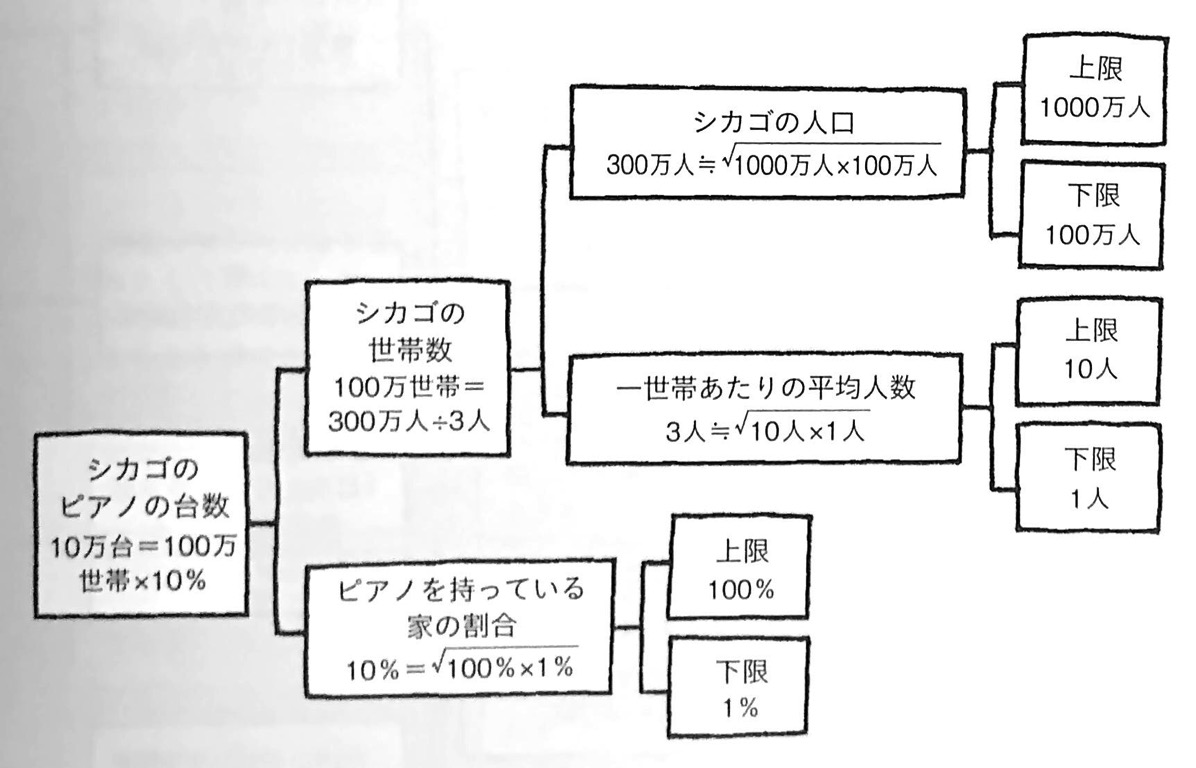
そこで下限と上限を設定し、シカゴの人口は100万人〜1000万人の間にある、と仮定しよう。我々は桁数にだけ関心があるから、100万と1000万の間をとるのに幾何平均を使う。◎桁が2桁異なっているなら、ただその間の桁数にすればいい。1(=100)と100(=102)なら10(=101)ということだ。
◎桁が1桁異なっているなら、下の桁を採用して3を掛ける。たとえば10と100なら30になる。√10≒3(だいたい3)だから、本当は√10×100=√101×102=√10×10=31.62・・・くらいになるのだが、最上位の1桁だけわかればいいという方針だから30でいい。√106×107を計算するわけだが、ざっくり300万人だとしても、我々が求める精度では問題ない。
これでシカゴの人口が、極めて大雑把にだが見積もれた。
この方法では、桁数がわかればいい、という割り切りから導き出されるものだが、とても活用範囲が広い。
基本となる数値がわからないときは、多くの場合、この方法で切り抜けられる。
たとえばシカゴの1世帯あたりの平均人数がわからないとする。
今の方法を用いるなら、下限:1人(単身者世帯ってある。それもけっこうある)
上限:10人(何十人って家族はいまどきは珍しい。都市だともっと珍しい)
1と10の幾何平均をとって3人を平均世帯数として採用できる(√1×10≒3)。
最後にピアノを持つ家の割合も考えておこう。
下限を1%とする。つまり0%(シカゴのどの家もピアノを持ってない)ってことはさすがにないと考えたのである。
上限を100%とする。つまりすべての家がピアノを持っているのが、どう考えても上限である。
これを幾何平均を取ると10%となる。④分割した推定を掛け合わせて答えを出す。
『問題解決大全』 第1部 より 読書猿:著 フォレスト出版:刊
おおよその数字でいいから、すぐに知りたい。
そんなときに、とても便利な方法です。
時間のあるときに、いろいろな数字を推定してみる。
それも「頭の体操」として、楽しめそうですね。
「意志の力」に頼らないための方法
「明日からやろう」と決意する。
しかし、次の日には、それを無視して、それまで通りの生活を送ってしまう。
多くの人が経験したパターンでしょう。
その原因のひとつに、「動学的不整合性」があります。
動学的不整合性は、目的を達成する行動を決定する場合に、現在の時点で最も望ましいとされた行動が、将来の時点では望ましくなく(言い換えれば他の行動が最も望ましく)なり、事前の決定が覆されてしまう性質
のことです。
長期的なスキルや習慣を身につける。
そのためには、この動学的不整合性と、どう向き合うかがポイントになります。
この動学的不整合の問題に対処するために選択肢を減らすというアプローチは、古代ギリシャの叙事詩『オデュッセイア』にある次のエピソードにまで遡(さかのぼ)る。
伝説の島アイアイエーに住む魔女キルケーの下で1年を過ごした後、島から旅立とうとするオデュッセウスに対して、道中の無事を願うキルケーは、セイレーンの海域では魔力のある彼女たちの歌を聴いてはならないと忠告する。なぜなら、セイレーンの歌を聴いたものは皆心を奪われ、自らその歌声に近づき、死ぬまでそこに留まることになるからである。
しかしキルケーは、知的好奇心のかたまりであるオデュッセウスが、セイレーンの歌を聴くに違いないとも思っていた。そこで忠告だけではなく、具体的な対策までも提示してくれたのである。すなわち、①部下たちの耳の穴を蜜蝋で塞ぎ、彼らは決してセイレーンの声聴くことがないようすること。
②セイレーンの歌声を聴きたいであろうオデュッセウスに対しては、帆柱の根本に手と足を縛りつけておくこと。
③そしてセイレーンの歌声を聴いたオデュッセウスが「縄を解いてくれ」と頼んだら、部下たちには一層きつく縛りつけるよう、事前に申しつけておくこと。キルケーの館から出発し、オデュッセウスたちの船はセイレーンがいる島の傍らを通過する。案の定、オデュッセウスはセイレーンの歌声に心奪われ、セイレーンの島に進むのだと叫ぶが、仲間たちは歌もその言葉も聞こえず、歌声が聞こえない安全な海域までそのまま無視して進み危機を切り抜けた。
我々凡人と、古代ギリシアの知将オデュッセウスの違いは、彼が自分の意志の力をあてにしなかったことだ。
そこには人間の本質についての冷徹な知見があった。
いざとなれば、ヒトの認知は、当初の決意も想定も裏切る。かつての取り決めがたとえどんなに合理的で長期に利益を約束していても、我々は目下の刺激を最大限に評価して決断し行動する。『問題解決大全』 第1部 より 読書猿:著 フォレスト出版:刊
動学的不整合性の罠は、「自分には意志力がある」と信じている人ほど、陥りやすいといえます。
人間の意志の力は、そのときの状況次第で、大きく変わります。
意志の力に頼らずに、行動できる仕組みを築くのが、最善の策だということですね。
「解き終えた直後」が、最上の学びのとき
ある問題を解いたあとに、再び、同じ問題を最初から解く。
これを、解ができる限り、明確かつ直接的になるまで繰り返す
。
そうして導き出された「ルール」は、永久に価値のあるものになることが多い
とのこと。
問題解決は、そもそもコストの高い行為である。
最低でも多くの認知資源と二度と戻らない多くの時間が費やされる。
大抵の場合、さらに資金や権限、多くの人の参加・協力が必要になる。そして極めつけは、成功は必ずしも約束されているわけではないことである。
その上、さらに問題を解き直すのは、贅沢な行為だ。
それゆえに解き直しは、自分の頭脳だけあれば足りるような問題解決で、すなわち数学やその隣接分野で、主に行われてきた。
なぜ(わさわざ)、解き終えた問題にもう一度取り組むのか?
その理由は人は自分がやった問題解決であっても、そのすべてを理解してはいないからである。問題解決に何が有効であり何がそうでなかっかたかを見極めるのには距離をとる必要がある。投じた努力の意義と意味、自分自身の内に生まれたインスピレーションの含意を理解するには時間がかかる。
それらの本当の果実は、まだ収穫されていないのである。
(中略)
問題解決を学んでいると(問題解決の書物を読んでいると)しばしば忘れがちだが、我々が出会う問題の多くは、実のところ解答不能である。そもそも解くべきでない問題も少なくない。
これに対して、二度目に解く者に約束されたものが1つある。それはその問題が解決可能であることだ。
一度目に解くのと二度目に以降の大きな違いは、その問題が解決可能かどうかを知らないのと知っているのとの差である。
また二度目の問題解決は、たいていは一度目のときよりずっと速やかに進み、労は少なく益が多い。二度目であればこそ、一度目では気づかなかったアイデアやアプローチを思いつける。ことによると、一度目では到達し得なかった解決を発見できる可能性すらある。
なんとなれば、我々はすでに問題について熟知しており、加えてその問題において解決がどんなものなのか、そもそも解決があるのかについても今や多くを知っている。試行錯誤の多くの枝ははらわれ、一度目には選択肢(オプション)とならなかったアプローチへのチャレンジも可能になる。
そして、立ち塞がっていた問題は、解決にたどり着いた今、長く厳しい問題解決をともに戦った戦友となっている。『問題解決大全』 第1部 より 読書猿:著 フォレスト出版:刊
読書猿さんは、自分がやった問題解決自体が、最良のメンターになる
と述べています。
問題解決さえ、できればいい。
と、せっかく努力した解決までの過程を、すべて捨ててしまうのは、もったいないですね。
同じような問題と対峙したとき、それまでの経験を活かす。
そのためにも、問題の解き直しによる、ブラッシュアップは欠かすことはできません。
[ad#kiji-shita-1]
☆ ★ ☆ ★ ☆ ★ ☆
世の中、解決すべき問題や課題は、山積されています。
それどころか、誰も、その全体像が摑めないほど、膨れ上がっているのが実情です。
問題や課題は、すべて違う“顔”をしています。
しかし、その本質的な部分は、似通っているものも、数多くあります。
人間の本質は、そう簡単に変わるものではありません。
そうである以上、人間の抱える悩みや欲も、同じようなものになるのは、当たり前といえます。
有史以来、人類が積み重ねてきた、問題解決への挑戦の数々。
それらは、私たち一人一人が、人生で課題に直面したときにも、役立つものです。
本書は、問題解決の方法に特化したツールを詰め込んだ、まさに“工具箱”のような優れものです。
一家に一台、いや一冊。
もしものときのため、ぜひ、用意しておきたいです。
![]() (←気に入ってもらえたら、左のボタンを押して頂けると嬉しいです)
(←気に入ってもらえたら、左のボタンを押して頂けると嬉しいです)
【書評】『アマゾンが描く2022年の世界』(田中道昭) 【書評】『いまさら聞けない ビットコインとブロックチェーン』(大塚雄介)